decToBin関数

本ページには広告が含まれています。

10進数を2進数に変換します。2進数を10進数に変換するにはbinToDec関数 (自作関数)を使います。

構文
  1. UString = decToBin( dec, signFlg, digits )
引数
dec （Double）必須
10進数
signFlg （Boolean = False）省略可
符号付きならばTrueを指定
digits （Boolean = False,Double = False）省略可
変換した2進数の桁数合わせを自動で行うかを示すブール値、もしくは桁数を表す数値（8,16,24,32,64のいずれか）を指定
戻り値
2進数に変換した値

プログラム

UWSC
//////////////////////////////////////////////////
// 【引数】
//   dec : 10進数 
//   signFlg : 符号付きならばTrueを指定 
//   digits : 変換した2進数の桁数合わせを自動で行うかを示すブール値、もしくは桁数を表す数値（8,16,24,32,64のいずれか）を指定 
// 【戻り値】
//   2進数に変換した値 
//////////////////////////////////////////////////
FUNCTION decToBin(dec, signFlg = FALSE, digits = FALSE)
	// 負数で符号なしならばエラー値を返す
	IFB dec < 0 AND signFlg = FALSE THEN
		PRINT "負数の場合signFlgにTrueを指定してください"
		RESULT = ERR_VALUE
		EXIT
	ENDIF
	
	// digitsのビット数が足りなければエラー値を返す、負数なら1桁多く取る
	IFB VARTYPE(digits) <> VAR_BOOLEAN AND digits < CEIL(LOGN(2, ABS(dec))) + IIF(dec < 0, 1, 0) THEN
		PRINT "ビット数が足りません"
		RESULT = ERR_VALUE
		EXIT
	ENDIF
	
	// signFlgがTrueかつdigitsがFalseならばエラー値を返す
	IFB signFlg AND !digits THEN
		PRINT "signFlgがTrueのときdigitsはFalse以外を選択してください"
		RESULT = ERR_VALUE
		EXIT
	ENDIF

	// bin：2進数に変換した結果を代入する変数
	DIM bin = ""
	DIM decimalFlg = IIF(POS(".", dec) <> 0, TRUE, FALSE)
	DIM negativeFlg = IIF(dec < 0, TRUE, FALSE)
	dec = ABS(dec)
	
	// (1) 10進数を整数部と小数部に分ける
	DIM integer = IIF(decimalFlg, COPY(dec, 1, POS(".", dec) - 1), dec)
	DIM decimal = IIF(decimalFlg, "0." + COPY(dec, POS(".", dec) + 1), 0)

	// (2) 10進数（整数部）を2進数に変換する。
	REPEAT
		bin = (integer MOD 2) + bin
		integer = INT(integer / 2)
	UNTIL integer = 0

	// (3) 10進数（小数部）を2進数に変換する。
	IFB decimalFlg THEN
		bin = bin + "."
		DIM loop = 0
		REPEAT
			loop = loop + 1
			decimal = decimal * 2
			bin = bin + IIF(decimal >= 1, "1", "0")
			IF decimal > 1 THEN decimal = decimal - 1
		UNTIL decimal = 1 OR loop > 64
	ENDIF

	// digitsがFALSE以外なら
	IFB digits THEN
		// (4) 2進数の桁合わせを行う
		DIM tmp = bin
		DIM binInteger = TOKEN(".", tmp)
		DIM binDecimal = TOKEN(".", tmp)
		// 整数部、小数部を4bit単位になるまで拡張
		// 整数部、4の倍数になるまで整数部の先頭に'0'を追加
		IF LENGTH(binInteger) MOD 4 <> 0 THEN binInteger = strRepeat("0", 4 - LENGTH(binInteger) MOD 4) + binInteger
		// 小数部、4の倍数になるまで小数部の末尾に'0'を追加
		IF LENGTH(binDecimal) MOD 4 <> 0 THEN binDecimal = binDecimal + strRepeat("0", 4 - LENGTH(binDecimal) MOD 4)
		DIM digit = LENGTH(binInteger + binDecimal)

		// 10進数の場合、一旦自動調整を行う
		integer = INT(dec)

		IF signFlg AND COPY(binInteger, 1, 1) = "1" THEN binInteger = strRepeat("0", 4) + binInteger

		IFB signFlg THEN
			IFB integer >= -128 AND integer <= 127 THEN						// -2^7〜2^7-1
				binInteger = strRepeat("0", 8 - LENGTH(binInteger)) + binInteger
			ELSEIF integer >= -32768 AND integer <= 32767 THEN				// -2^15〜2^15-1
				binInteger = strRepeat("0", 16 - LENGTH(binInteger)) + binInteger
			ELSEIF integer >= -8388608 AND integer <= 8388607 THEN			// -2^23〜2^23-1
				binInteger = strRepeat("0", 24 - LENGTH(binInteger)) + binInteger
			ELSEIF integer >= -2147783648 AND integer <= 2147483647 THEN	// -2^31〜2^31-1
				binInteger = strRepeat("0", 32 - LENGTH(binInteger)) + binInteger
			ELSE
				binInteger = strRepeat("0", 64 - LENGTH(binInteger)) + binInteger
			ENDIF
		ELSE
			IFB integer <= 255 THEN				// 2^8-1
				binInteger = strRepeat("0", 8 - LENGTH(binInteger)) + binInteger		
			ELSEIF integer <= 65535 THEN		// 2^16-1
				binInteger = strRepeat("0", 16 - LENGTH(binInteger)) + binInteger		
			ELSEIF integer <= 16777215 THEN		// 2^24-1
				binInteger = strRepeat("0", 24 - LENGTH(binInteger)) + binInteger
			ELSEIF integer <= 4294967295 THEN	// 2^32-1
				binInteger = strRepeat("0", 32 - LENGTH(binInteger)) + binInteger
			ELSE
				binInteger = strRepeat("0", 64 - LENGTH(binInteger)) + binInteger
			ENDIF
		ENDIF

		totalDigits = LENGTH(binInteger + binDecimal)

		IFB totalDigits > 64 THEN
			DIM del32 = totalDigits - 32
			DIM del64 = totalDigits - 64
			IFB del32 = LENGTH(binDecimal) AND digits <> 64 THEN
				binDecimal = ""
				PRINT "32bitを超えたため、小数点以下を削除しました"
			ELSEIF del32 < LENGTH(binDecimal) AND digits <> 64 THEN
				binDecimal = COPY(binDecimal, 1, LENGTH(binDecimal) - del32)
				PRINT "32bitを超えたため、小数点以下の一部を削除しました"
			ELSEIF del64 = LENGTH(binDecimal) AND del64 <> 0 THEN
				binDecimal = ""
				PRINT "64bitを超えたため、小数点以下を削除しました"
			ELSEIF del64 < LENGTH(binDecimal) THEN
				binDecimal = COPY(binDecimal, 1, LENGTH(binDecimal) - del64)
				PRINT "64bitを超えたため、小数点以下の一部を削除しました"
			ELSE
				RESULT = ERR_VALUE
				PRINT "64bitを超えるため、変換できません"
				EXIT
			ENDIF
		ENDIF

		// 整数部、小数部の合計桁数を8,16,24,32,64bit単位になるまで拡張
		digit = LENGTH(binInteger + binDecimal)
		DIM array[] = 8, 16, 24, 32, 64
		FOR item IN array
			IFB digit <= item THEN
				binInteger = strRepeat("0", item - digit) + binInteger
				BREAK
			ENDIF
		NEXT

		// 指定ビットに調整
		// 合計桁数の再設定
		totalDigits = LENGTH(binInteger + binDecimal)
		
		IFB digits = TRUE THEN
			// 桁合わせを自動調整
			IFB totalDigits > 64 THEN
				len = LENGTH(binInteger + binDecimal)
				WHILE LENGTH(binInteger) > 8 AND len > digits
					IFB COPY(binInteger, 1, 4) = "0000" THEN
						binInteger = COPY(binInteger, 5)
						len = len - 4
					ELSE
						BREAK
					ENDIF
				WEND
	
				WHILE LENGTH(binDecimal) > 4 AND LENGTH(binInteger + binDecimal) > digits
				IFB COPY(binDecimal, LENGTH(binDecimal) - 4) = "0000" THEN
					binDecimal = COPY(binDecimal, 1, LENGTH(binDecimal) - 4)
					ELSE
						BREAK
					ENDIF
				WEND
				tmp = binInteger + "." + binDecimal

				binInteger = COPY(tmp, 1, POS(".", tmp) - 1)
				binDecimal = COPY(tmp, POS(".", tmp) + 1)
				totalDigits = LENGTH(binInteger + binDecimal)
				IFB totalDigits > 64 THEN
					RESULT = ERR_VALUE
					PRINT "64bitを超えたため変換できません"
					EXIT
				ENDIF
			ENDIF
		ELSE
			// 指定ビットに調整
			IFB totalDigits <= digits THEN
				binInteger = strPad(binInteger, digits - LENGTH(binDecimal), "0", LEFT)
			ELSE
				// 桁あふれ調整
				totalDigits = LENGTH(binInteger + binDecimal)

				len = LENGTH(binInteger + binDecimal)
				WHILE LENGTH(binInteger) > 8 AND len > digits
					IFB COPY(binInteger, 1, 4) = "0000" THEN
						binInteger = COPY(binInteger, 5)
						len = len - 4
					ELSE
						BREAK
					ENDIF
				WEND
	
				WHILE LENGTH(binDecimal) > 4 AND LENGTH(binInteger + binDecimal) > digits
				IFB COPY(binDecimal, LENGTH(binDecimal) - 4) = "0000" THEN
					binDecimal = COPY(binDecimal, 1, LENGTH(binDecimal) - 4)
					ELSE
						BREAK
					ENDIF
				WEND
				tmp = binInteger + "." + binDecimal

				binInteger = COPY(tmp, 1, POS(".", tmp) - 1)
				binDecimal = COPY(tmp, POS(".", tmp) + 1)
				len = LENGTH(binInteger + binDecimal)
				IFB len > digits THEN
					DIM deleteLength = len - digits
					IFB deleteLength = LENGTH(binDecimal) THEN
						binDecimal = ""
						PRINT "指定ビット数にするため小数点以下を削除しました"
					ELSEIF deleteLength < LENGTH(binDecimal) THEN
						binDecimal = COPY(binDecimal, 1, LENGTH(binDecimal) - deleteLength)
						PRINT "指定ビット数にするため小数点以下の一部を削除しました"
					ELSE
						RESULT = ERR_VALUE
						PRINT "指定ビット数では変換できません"
						EXIT
					ENDIF
				ENDIF
			ENDIF
		ENDIF

		bin = binInteger + IIF(binDecimal <> "", "." + binDecimal, "")

		// (5) 入力値がマイナスのため、2進数をマイナス値に変換する
		IFB negativeFlg THEN
			// 1の補数
			bin = bitNot(bin)
			// 2の補数
			DIM res = ""
			DIM carry = "1"
			FOR i = LENGTH(bin) TO 1 STEP -1
				IFB carry = "1" THEN
					SELECT COPY(bin, i, 1)
						CASE "0"
							res = "1" + res
							carry = 0
						CASE "1"
							res = "0" + res
						DEFAULT
							res = COPY(bin, i, 1) + res
					SELEND
				ELSE
					res = COPY(bin, i, 1) + res
				ENDIF
			NEXT
			bin = res
		ENDIF
	ENDIF
	RESULT = bin
FEND

//////////////////////////////////////////////////
// 【引数】
//   num : 10進数もしくは2進数の値 
//   bit : ビット 
// 【戻り値】
//   ビットを反転した値 
//////////////////////////////////////////////////
FUNCTION bitNot(num, bit = EMPTY)
	IFB isString(num) THEN
		DIM res = ""
		FOR i = 1 TO LENGTH(num)
			DIM str = COPY(num, i, 1)
			IFB str = "0" OR str = "1" THEN
				res = res + (1 - VAL(str))
			ELSE
				res = res + str
			ENDIF
		NEXT
		RESULT = res
	ELSE
		DIM exponent = IIF(bit = EMPTY, CEIL(LOGN(2, num + 1)), bit)
		RESULT = POWER(2, exponent) - num - 1
	ENDIF
FEND

//////////////////////////////////////////////////
// 【引数】
//   expr : 評価する式 
//   truepart : 評価した式がTrueのときに返す値 
//   falsepart : 評価した式がFalseのときに返す値 
// 【戻り値】
//   truepart : 評価した式がTrueのとき、falsepart : 評価した式がFalseのとき 
//////////////////////////////////////////////////
FUNCTION IIF(expr, truepart, falsepart)
	IFB EVAL(expr) THEN
		RESULT = truepart
	ELSE
		RESULT = falsepart
	ENDIF
FEND

//////////////////////////////////////////////////
// 【引数】
//   variable : 型を調べる変数 
// 【戻り値】
//    : TRUE : 与えられた変数が文字列型である、 
//   FALSE : 与えられた変数が文字列型でない、 : 
//////////////////////////////////////////////////
FUNCTION isString(variable)
	RESULT = IIF(VARTYPE(variable) = VAR_ASTR OR VARTYPE(variable) = VAR_USTR, TRUE, FALSE)
FEND

//////////////////////////////////////////////////
// 【引数】
//   num : 符号を求める数値 
// 【戻り値】
//   1 : 正の数、0 : ゼロ、-1 : 負の数、ERR_VALUE : それ以外 
//////////////////////////////////////////////////
FUNCTION sign(num)
	SELECT TRUE
		CASE !CHKNUM(num)
			RESULT = ERR_VALUE
		CASE num > 0
			RESULT = 1
		CASE num = 0
			RESULT = 0
		CASE num < 0
			RESULT = -1
	SELEND
FEND

//////////////////////////////////////////////////
// 【引数】
//   input : 入力文字列 
//   length : 埋めたあとの長さ 
//   str : 埋める文字 
//   type : 埋める方向 
// 【戻り値】
//   指定文字で埋めた文字列 
//////////////////////////////////////////////////
FUNCTION strPad(input, length, str = " ", type = RIGHT)
	DIM s = ""
	SELECT type
		CASE LEFT
			FOR i = 1 TO CEIL((length - LENGTH(input)) / LENGTH(str))
				s = s + str
			NEXT
			input = COPY(s, 1, length - LENGTH(input)) + input
		CASE RIGHT
			FOR i = 1 TO CEIL((length - LENGTH(input)) / LENGTH(str))
				s = s + str
			NEXT
			input = input + COPY(s, 1, length - LENGTH(input))
	SELEND
	RESULT = input
FEND

//////////////////////////////////////////////////
// 【引数】
//   inputs : 繰り返す文字列 
//   multiplier : inputsを繰り返す回数 
// 【戻り値】
//   inputsをmultiplier回を繰り返した文字列を返します 
//////////////////////////////////////////////////
FUNCTION strRepeat(inputs, multiplier)
	DIM res = ""
	FOR n = 1 TO multiplier
		res = res + inputs
	NEXT
	RESULT = res
FEND

10進数から2進数への変換方法

整数部を変換

  1. 整数部を2で割り、商と余りを求める。
  2. 商をさらに2で割り、商と余りを求める手順を商が0になるまで繰り返す。
  3. 求めた余りを下位桁から並べたものが2進数の値となります。

197の場合、以下のように求めることができ11000101となります。

10進数を2進数に変換

小数部を変換

10進数の値が小数の場合、以下の手順を行います。

  1. まず小数部の先頭に0.を補い、0.XXXXXの形式にします。この値に2を掛け、結果を整数部と小数部に分けます。
  2. この処理を小数部が0になるまで繰り返し、整数部を上位桁から並べた値が2進数の値になります。

0.8125の場合、以下のように求めることができ0.1101となります。

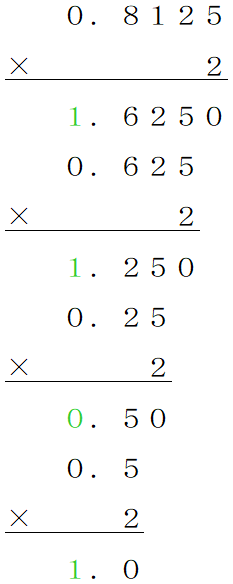
10進数→2進数 小数部.png

符号付き

10進数の場合符号で正負を判断することができますが、2進数の場合は符号ではなく最上位ビット（最も左のビット）で正負を判断します。signFlgにTrueを指定した場合、最上位ビットが0の場合はプラス、1の場合はマイナスを表します。

桁数合わせ

digitsにTrueを指定した場合、2進数に変換した値を8、16、24、32、64のビット数の中から表現できる最小のビット数で表します。

digitsに数値を指定した場合はそのビット数で表現しますが、ビット数が足りない場合はエラー値（ERR_VALUE）を返します。またdigitsにFalseが指定された場合は桁数合わせを行いません。

桁数合わせは以下の手順で行われます。

  1. 整数部分と小数部分に分け、それぞれ4桁の倍数になるようにゼロ埋めを行う。
  2. 符号ありの場合-128〜127で8桁、-32768〜32767で16桁、-8388608〜8388607で24桁、-2147783648〜2147783647で32桁、それ以外の値は64桁になるようゼロ埋めします。符号なしの場合255以下で8桁、65535以下で16桁、16777215以下で24桁、4294967295以下で32桁、それ以上の値は64桁になるようゼロ埋めします。

桁数合わせは、まず整数部分と小数部分それぞれで4桁の倍数になるようにゼロ埋めを行います。その後全体の桁数が、8、16、24、32、64になるように整数部分の左側を0埋めします。

そのため整数値の場合は最低8桁、小数値の場合は最低16桁になります。

以下は桁合わせの有無による結果の違いを表したものです。

UWSC
PRINT decToBin(5.5)
PRINT decToBin(5.5, TRUE, TRUE)
PRINT "-----"
PRINT decToBin(2.96875)
PRINT decToBin(2.96875, TRUE, TRUE)
PRINT "-----"
PRINT decToBin(1.9404296875)
PRINT decToBin(1.9404296875, TRUE, TRUE)
結果
プレーンテキスト
101.1
000000000101.1000
-----
10.11111
00000010.11111000
-----
1.1111000011
000000000001.111100001100

5.5は2進数に変換した結果101.1を整数部分（101）と小数部分（1）に分けます。

2の補数を求める（負数のみ）

ビットを反転して1の補数を求めます。1の補数の最下位ビットに1を加えることで2の補数を求めることができます。

使い方

10進数の整数を2進数に変換

10進数の5、31、405、56825、4666818、1234567890をそれぞれ2進数に変換します。

第一引数のみを指定したときは符号なし、桁数合わせなしで変換されます。桁数合わせなしはゼロ埋めをしないので左端は必ず1になります。

UWSC
PRINT decToBin(5)
PRINT decToBin(31)
PRINT decToBin(405)
PRINT decToBin(56825)
PRINT decToBin(4666818)
PRINT decToBin(1234567890)
結果
プレーンテキスト
101
11111
110010101
1101110111111001
10001110011010111000010
1001001100101100000001011010010

10進数の整数を符号付きで2進数に変換

負数を2進数に変換するときは第一引数に負数を指定するだけではエラーが発生します。

UWSC
PRINT decToBin(-12)
結果
プレーンテキスト
負数の場合signFlgにTrueを指定してください
-999999

負数を指定する場合、第二引数にTrue、第三引数にFalse以外の値を指定する必要があります。

以下は-12を桁数合わせを自動調整で2進数に変換するプログラムです。

UWSC
PRINT decToBin(-12, TRUE, TRUE)
結果
プレーンテキスト
11110100

指定した桁数の2進数に変換するには、第三引数に数値を指定します。

以下は-12を2進数で桁数を8、16、24、32、64で表現するプログラムです。

UWSC
PRINT decToBin(-12, TRUE, 8)
PRINT decToBin(-12, TRUE, 16)
PRINT decToBin(-12, TRUE, 24)
PRINT decToBin(-12, TRUE, 32)
PRINT decToBin(-12, TRUE, 64)
結果
プレーンテキスト
11110100
1111111111110100
111111111111111111110100
11111111111111111111111111110100
1111111111111111111111111111111111111111111111111111111111110100

10進数の11を符号付き、桁数合わせを自動調整で2進数に変換します。

自動調整のとき桁数は8、16、24、32、64の中で表現できる最小の桁数となります。11を符号なしで変換したときは1011と4桁になるので、最小の8桁で表現されます。

UWSC
PRINT decToBin(11, TRUE, TRUE)
結果
プレーンテキスト
00001011

10進数の整数を符号なしで2進数に変換

10進数の65536を符号なし、桁数合わせ自動調整で2進数に変換します。

10進数の65536は2進数に変換すると1 0000 0000 0000 0000と17桁になるので、24桁まで左側をゼロ埋めされます。

UWSC
PRINT decToBin(65536, FALSE, TRUE)
結果
プレーンテキスト
000000010000000000000000

桁数自動調整で2進数に変換

以下は10進数の255を符号付き、桁数自動調整で2進数に変換するプログラムです。

10進数の255を2進数に変換すると1111 1111と8桁の値になります。符号なしの場合、先頭ビットの値は関係ないので結果は1111 1111となります。

符号付きのときは先頭ビットが0で正数、1で負数を表します。もとの10進数の値が255と正数のため先頭に0を付与し正数とします。符号なしの結果に0を付与すると0 1111 1111で9桁になるため、最小の桁数は16桁で自動調整され結果は0000 0000 1111 1111となります。

UWSC
PRINT decToBin(255, FALSE, TRUE)
PRINT decToBin(255, TRUE, TRUE)
結果
プレーンテキスト
11111111
0000000011111111

ビット数が足りない場合はエラー値（ERR_VALUE）を返します。10進数の65536は2進数では1 0000 0000 0000 0000となり17桁以上必要なので8桁では表現出来ずエラーが発生します。

UWSC
PRINT decToBin(65536, TRUE, 8)
結果
プレーンテキスト
ビット数が足りません
-999999

10進数の整数を符号なしで2進数に変換

10進数の255を符号なし、桁数自動調整で2進数に変換します。

符号なしの場合先頭で符号を表現する必要がないので8桁で表現されます。

UWSC
PRINT decToBin(255, FALSE, TRUE)
結果
プレーンテキスト
11111111

10進数の小数を2進数に変換

10進数の250.125を2進数に変換します。

UWSC
PRINT decToBin(250.125, FALSE, FALSE)
結果
プレーンテキスト
11111010.001

10進数の12.3を2進数に変換します。

10進数の小数を2進数に変換するとき、ほとんどの値で無限小数となるので正確に変換することができません。

UWSC
PRINT decToBin(12.3, TRUE, TRUE)
結果
プレーンテキスト
32bitを超えたため、小数点以下の一部を削除しました
00001100.010011001100110011001100

桁数合わせを自動調整にした場合、整数部と小数部合わせて32ビットで表現されます。64ビットで表現するにはdigitsに64を指定します。

UWSC
PRINT decToBin(12.3, TRUE, 64)
結果
プレーンテキスト
64bitを超えたため、小数点以下の一部を削除しました
00001100.01001100110011001100110011001100110011001100110011001100

関連記事

binToDec関数 (自作関数)
2進数を10進数に変換します。負数・小数の値にも対応しています。
binToHex関数 (自作関数)
2進数を16進数に変換します。16進数を2進数に変換するにはhexToBin関数を使います。
hexToBin関数 (自作関数)
16進数を2進数に変換します。2進数を16進数に変換するにはbinToHex関数を使います。
hexToDec関数 (自作関数)
16進数を10進数に変換します。10進数を16進数に変換するにはdecToHex関数を使います。
decToHex関数 (自作関数)
10進数を16進数に変換します。16進数を10進数に変換するにはhexToDec関数を使います。
radToDeg関数 (自作関数)
弧度法（Radian）を度数法（Degree）に変換します。度数法を弧度法に変換するにはDegToRad関数を使います。
degToRad関数 (自作関数)
度数法（Degree）を弧度法（Radian）に変換します。弧度法を度数法に変換するにはRadToDeg関数を使います。
ARABIC関数 (自作関数)
ARABIC関数は、ローマ数字をアラビア数字に変換する関数です。アラビア数字をローマ数字に変換するには、ROMAN関数を使います。
ROMAN関数 (自作関数)
ROMAN関数は、アラビア数字をローマ数字に変換する関数です。ローマ数字をアラビア数字に変換するには、ARABIC関数を使います。
16進数