目次
- 1 変数とは
- 2 変数の宣言を強制する
- 3 変数の適用範囲(スコープ)
- 4 変数の生存期間(有効期間)
- 5 変数名の付け方
- 6 ハンガリアン記法
- 7 2の補数
- 8 データ型とは
- 9 Empty/Empty
- 10 Null/Null
- 11 2バイト整数(符号付き)/SmallInt
- 12 4バイト整数(符号付き)/Integer
- 13 単精度浮動小数点数/Single
- 14 倍精度浮動小数点数/Double
- 15 通貨型/Currency
- 16 日付型/Date
- 17 オブジェクト型/Dispatch
- 18 ブール型/Boolean
- 19 1バイト整数(符号付き)/SByte
- 20 1バイト整数(符号なし)/Byte
- 21 2バイト整数(符号なし)/Word
- 22 4バイト整数(符号なし)/DWord
- 23 8バイト整数(符号付き)/Int64
- 24 ANSI文字列/AStr
- 25 UNICODE文字列/UStr
- 26 配列/Array
- 27 使い方
- 28 型変換
- 29 参考文献
変数とは
変数とは、プログラム中でデータを一時的に記憶しておく領域のことです。変数には固有の名前をつけることができ、その変数の名前を変数名といいます。プログラム中で何度も同じデータを参照するときに使います。
変数を使う例として、半径から円の直径と円周の長さを求めるプログラムを書いてみます。円の直径は半径×2、円周の長さは半径×2×3.14で求めることができ、以下のようなプログラムを書くことができます。
PRINT "半径5の円の直径:" + (5 * 2)
PRINT "半径5の円周の長さ:" + (5 * 2 * 3.14)このとき直径を求める式である5×2という部分が共通していて2回書かれていることがわかると思います。
このようにプログラム内で何度か出てくる式や値は、変数を使うと以下のように書くことができます。diameterは直径を意味する英単語です。
DIM diameter = 5 * 2
PRINT "半径5の円の直径:" + diameter
PRINT "半径5の円周の長さ:" + (diameter * 3.14)このプログラムではあまり変数を使う必要を感じない人もいるかもしれませんが、変数を使うメリットについて以下に示しておきます。
- 再利用性
- 変数を使うことで同じ値を何度も書く必要がなくなり、コードの記述量が減ります。例えば円周率を表すpiに3.14と代入しておけば、円周や円の面積を求めるときに円周率の値はpiと記述するだけで良くなります。
- 可読性
- 変数に適切な名前を付けていればコードの内容がとても読みやすくなります。自分または他の開発者がコードを理解しやすくなり、バグや修正が容易にできます。商品の単価にprice、数量にnumという変数名を付ければ、price * numが合計金額を表していることは一目瞭然です。
- 保守性
- まず保守性とは、ソフトウェアの仕様が変わったときに必要な修正や変更のしやすやを意味しています。例えば税抜金額から税込金額を求めるプログラムで商品単価 * 1.08のような処理をたくさん書いていた場合、消費税が8%から10%に上がったときに1.08をすべて1.10に書き換えなければなりません。このときに消費税率を表す変数をtax = 1.08と宣言していれば、消費税率が上がったときにこのtaxの値をtax = 1.10のように変更するだけで良くなります。
宣言
プログラムの中でどのような名前の変数を使用するのかを明示することを宣言といいます。
UWSCでは使用する変数の前にDIMまたはPUBLICをつけることで、その変数を宣言することができます。詳しい使い方はDIM、PUBLICを参考にしてください。
変数の宣言は省略することができ、その場合は初めて変数の代入が行われるときに宣言が自動的に行われます。変数の宣言を強制したい場合はOPTION指定を使い、プログラムの先頭でOPTION EXPLICITを指定します。
UWSCでは他のプログラミング言語とは違い宣言時に変数の型を指定する必要がありません。
以下はnameという変数を宣言する例。
DIM name宣言と同時に代入を行うことを初期化といい、以下のように記述します。
DIM name = "佐藤"代入
変数に文字列や数値などのデータを入れることを代入といいます。UWSCでは宣言時に型を指定する必要がなく、代入するときの値で型が自動的に決まります。数値を代入したときはDouble型、文字列をしたときはUString型となります。
以下はiに12と代入する例。
i = 12iの値を現在の値から1だけ増やす。
i = i + 1代入は一度だけでなく必要があれば何度でも代入し直すことができます。
既に値が代入されている変数に値を代入すると、代入されている値は削除され、新たに代入した値のみ参照することができます。
num = 123 // 変数への代入(宣言を省略)
PRINT num // 「123」が出力される
num = 456 // 「123」は削除され「456」が代入される
PRINT num // 「456」が出力される代入できるものは文字列・数値だけでなく変数の値を代入・結合することもできます。
a = 12 // aに「12」を代入
b = 15 // bに「15」を代入
c = a + b // cに「a + b」の計算結果を代入
PRINT c // 「27」を出力参照
変数に格納されているデータを利用することを参照といいます。例えば変数に数値や文字列を代入した後、その変数を使って計算したり出力したりする場合、変数の参照を行っています。
参照は変数名を記述するだけで利用することができます。値を出力したい場合はPRINT文、表示するにはMSGBOX関数 (スクリプト関数)を使って記述します。
DIM num = 123
PRINT num
MSGBOX(num)- 結果
123
宣言していない変数を参照すると変数: <変数名>が定義されていませんとエラーが表示されます。
変数の宣言を強制する
長いプログラムを書いていると、変数名のタイプミスなどにより思った結果を得られないということがあります。このような事態を防ぐためにプログラムの先頭にOPTION指定をすることで変数の宣言を強制することができます。
OPTION EXPLICIT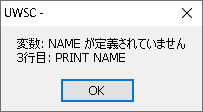
以下の場合nameを宣言し田中と代入したつもりが、実際にはnamaeに代入されていて何も出力されずエラーも発生しません。
DIM name
namae = "田中"
PRINT nameしかし以下のように宣言を強制すると、namaeは宣言されていないので実行時にエラーが発生しタイプミスがあることに気付けます。
OPTION EXPLICIT
DIM name
namae = "田中"
PRINT name変数の適用範囲(スコープ)
変数を使用できる範囲のことを変数の適用範囲または変数のスコープといいます。DIMでローカル変数を宣言した場合、メインルーチンで宣言したきはとメインルーチン内で、関数内で宣言された変数はその関数内でしか使用できません。
グローバル変数で宣言した変数は、プロセスの生成時に値の代入が行われ、メインルーチンが終了するまでの間どの場所でも代入・参照が行えます。
グローバル変数で宣言すればどこからでも参照・代入ができるので便利ですが、誤動作のもとになるため変数の参照が必要ない範囲での使用は控えるようにしましょう。
変数の生存期間(有効期間)
変数の生存期間とは、変数がメモリ上に存在し値をいつまで保持し続けるかの時間のことです。
変数の生存期間は変数の種類や場所によって異なります。例えば、グローバル変数はプログラムの開始から終了まで生存しますが、ローカル変数は宣言されたスコープ内でのみ生存します。
変数名の付け方
変数名を決める際、日本語からネーミングを生成してくれるcodic - プログラマーのためのネーミング辞書を使うととても便利です。
どの記法でなければならないという決まりはないので自分の使いやすい記法で良いですが、記法は統一しましょう。
- PascalCase
- 変数名に含まれる単語の頭文字をすべて大文字にする記法です。プログラミング言語Pascalで使われていた記法であることが由来。
例)UserId、CustomerName - camelCase
- 先頭を除くすべての単語の頭文字を大文字にする記法です。単語の並びがラクダ(camel)のこぶのように見えることが由来。
例)userId、customerName - snake_case
- 単語間を_(アンダースコア)でつなげる記法。単語はすべて小文字。蛇のように見えることが由来。
例)user_id、customer_name - SNAKE_CASE
- 単語間を_(アンダーバー)でつなげる記法。単語はすべて大文字。
例)USER_ID、CUSTOMER_NAME - ハイフネーション
- 単語間を-(ハイフン)でつなげる記法。ケバブケースとも言います。
例)user-id、customer-name - 変換なし
- 入力された日本語を英語にします。変数名に半角スペースは使えないので、おそらく英単語を確認するためのもの。
例)user id、customer name
以下は単語間の繋げ方のルールというよりは変数の意味をわかりやすくする+α的なもの。
- ハンガリアン(ハンガリー)
- 変数名・関数名などに接頭辞・接尾辞をつけることで、使用方法・データ型をわかるようにしたもの。この記法の考案者がハンガリー出身であることに由来。
変数名の例
以下に変数名としてよく使われる単語との意味を表にしておきます。
| 変数名 | 意味 |
|---|---|
| sum | 合計値 |
| str | 文字列 |
| filename | ファイル名 |
| folderspec | フォルダ名 |
| path | パス |
| time | 時間 |
| serial | シリアル値 |
| array | 配列 |
| x | x座標 |
| y | y座標 |
| source | HTMLソース |
| year | 年 |
| month | 月 |
| day | 日 |
| hour | 時間 |
| minute | 分 |
| second | 秒 |
| date | 日付 |
| weekday | 曜日 |
| rate | 割合 |
| メールアドレス | |
| username | ユーザー名 |
| msg | メッセージ |
| width | 幅 |
| height | 高さ |
| row | 行 |
| column | 列 |
| size | サイズ |
| bool | True or False(Boolean型) |
| flg | True or False(Boolean型) |
| cnt | カウント |
| i | カウンタ変数(For文、While文など) |
| age | 年齢 |
| birthday | 誕生日 |
| buf | 一時的な代入 |
| tmp | 一時的な代入 |
| ID | GETIDで取得したウィンドウID |
| bin | 2進数の値 |
| dec | 10進数の値 |
| hex | 16進数の値 |
| price | 価格 |
| encodeStr | エンコードした文字列 |
| decodeStr | デコードした文字列 |
| formula | 式 |
ハンガリアン記法
型を表す接頭辞
| 文字 | 意味 |
|---|---|
| bまたはf | 論理型 |
| ch | 文字型 |
| by | バイト型 |
| nまたはi | 整数型 |
| l | 長整数 |
| u | 符号なし整数 |
| w | ワード型 |
| dw | ダブルワード型 |
| fpまたはf | 単精度浮動小数点型 |
| dbまたはd | 倍精度浮動小数点型 |
| pまたはlp | ポインタ型 |
| s | 文字列型 |
| sz | ゼロ終端文字列型 |
| fn | 関数ポインタ型 |
| h | ハンドル型 |
| hwndまたはh | ウィンドウハンドル型 |
| g_ | グローバル変数 |
| c_ | 定数 |
| c_ | 静的変数 |
| m_ | クラスのメンバー変数 |
| C | クラス |
| tag | 構造体タグ |
2の補数
2の補数とは2進数で負の数を表すのに使われている方法です。2 の補数では先頭ビットが符号を表し、0の場合はプラス、1の場合はマイナスを表します。負の数を表す場合ビット数は固定して考えます。
2の補数(負の数)の作り方
- 符号を無視して2進数に変換する。
- 各ビットを反転させる。
- 最終ビットに1を加える。
-5を2進数4ビット固定で表す例。
符号を取り除いた5を2進数にする。
0101各ビットを反転。(0→1、1→0)
10101を加えた値が2の補数になります。
10112の補数からの戻し方
2の補数を作るときと逆の手順を行います。
- 2の補数から-1する。
- 各ビットを反転させる。
- 10進数にして先頭にマイナスをつける。
1011を戻す例。
1を引く。
1010各ビットを反転。(0→1、1→0)
101010進数にしてマイナスを付ける。
-5データ型とは
データ型とはプログラミング言語が扱うデータをいくつかの種類に分類し、どのように扱うかを定めたものです。整数型や文字列型などがあり、変数や値のデータ型に応じて適切な型を宣言します。
| 分類 | 型 | ||
|---|---|---|---|
| 数値型 | 整数型 | 符号付き | 1バイト整数(符号付き) |
| 2バイト整数(符号付き) | |||
| 4バイト整数(符号付き) | |||
| 8バイト整数(符号付き) | |||
| 符号なし | 1バイト整数(符号なし) | ||
| 2バイト整数(符号なし) | |||
| 4バイト整数(符号なし) | |||
| 浮動小数点数型 | 単精度浮動小数点数 | ||
| 倍精度浮動小数点数 | |||
| 固定小数点数型 | 通貨型 | ||
| 論理型 | ブール型 | ||
| 文字列型 | ANSI文字列 | ||
| UNICODE文字列 | |||
| 配列型 | 配列 | ||
整数型(数値型)
整数型とは整数を取り扱うためのデータ型で、ビット長や符号の有無によっていくつかの種類があります。
符号付き整数型
ビット数を\(n\)としたとき、符号付き整数型が扱える数値の範囲は以下の式で表すことができます。1バイトは8ビットです。
\[\begin{eqnarray} value_{min} &=& -2^{n-1} \\ value_{max} &=& 2^{n-1}-1 \end{eqnarray}\]- 1バイト整数(符号付き)
- -128~127までの数値を表すことができる型。
- 2バイト整数(符号付き)
- -32,768~32,767までの数値を表すことができる型。
- 4バイト整数(符号付き)
- -2,147,483,648~2,147,483,647(-21億4748万3648〜21億4748万3647)までの数値を表すことができる型。
- 8バイト整数(符号付き)
- -9,223,372,036,854,775,808~9,223,372,036,854,775,807(-922京3372兆368億5477万5808〜922京3372兆368億5477万5807)までの数値を表すことができる型。
符号なし整数型
ビットを\(n\)としたとき、符号なし整数型が扱える数値の範囲は以下の式で求めることができます。
\[ \begin{eqnarray} value_{min} &=& 0 \\ value_{max} &=& 2^{n}-1 \end{eqnarray} \]- 1バイト整数(符号なし)
- 0~255までの数値を表すことができる型。
- 2バイト整数(符号なし)
- 0~65,535までの数値を表すことができる型。
- 4バイト整数(符号なし)
- 0~4,294,967,295までの数値を表すことができる型。
浮動小数点型(数値型)
浮動小数点数とは、実数をコンピュータで処理するために有限桁の小数で近似値として扱う方式のことで、小数点の位置を固定せず自由に動かして小数を表現します。浮動小数点型のサイズは単精度と倍精度があり、単精度は4バイト、倍精度は8バイトで表されます。
浮動小数点数は以下の式で求めることができます。
\[value=(-1)^{s} \times 2^{e-b} \times (1.m)\]- \(s\):符号ビット
- \(e\):指数部
- \(b\):バイアス値
- \(m\):仮数部
- 単精度浮動小数点型
- 符号部1ビット、指数部8ビット、仮数部24ビットの32ビットで数値を表します。約7桁の有効数字を持つ数値を表すことができる型です。
- 倍精度浮動小数点型
- 符号部1ビット、指数部11ビット、仮数部52ビットの64ビットで数値を表します。約15桁の有効数字を持つ数値を表すことができる型です。
以下は単精度浮動小数点数と倍精度浮動小数点数についてまとめた表です。
| 単精度 | 倍精度 | |
|---|---|---|
| 符号のビット数 | 1 | 1 |
| 仮数部のビット数 | 23 | 52 |
| 指数部のビット数 | 8 | 11 |
| 全体のビット数 | 32(4バイト) | 64(8バイト) |
| バイアス値 | 127 | 1023 |
10進数を浮動小数点数にする例
+123.4を浮動小数点数で表す
10進数で+123.4を浮動小数点数で表すと以下のようになります。
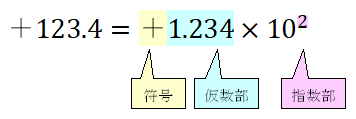
最も大きい位が1桁(\(1 \le x < 10\)の範囲)になるように小数点を動かします。この動かした桁数が指数部の値となります。左に動かした場合はプラス、右に動かした場合はマイナスになります。
123.4から小数点を左に2桁動かすと1.234になるので、指数部の値は2となります。
-0.001234を浮動小数点数で表す
続いて10進数の-0.001234を浮動小数点数で表すと以下のようになります。
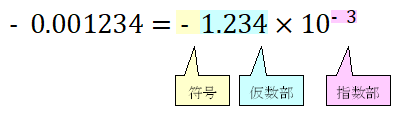
+123.4のときと同じように最も大きい位が1桁になるように小数点を動かします。
-0.001234から小数点を右に3桁動かすと-1.234になるので、指数部の値は-3となります。
このように符号、仮数部、指数部の3つで構成する書き方が浮動小数点数の表し方です。
2進数の浮動小数点
10進数では10を掛けることで桁を動かしましたが、2進数では2を掛けることで桁を動かすことができます。ここでは正負は符号で表すこととします。
\(+10.11_{(2)}\)を浮動小数点数で表す
2進数の+10.11を浮動小数点数で表すと以下のようになります。
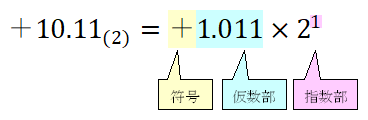
+10.11から小数点を左に1桁動かすと+1.011になるので指数部の値は1となります。
\(-0.01101_{(2)}\)を浮動小数点数で表す
2進数の-0.01101を浮動小数点数で表すと以下のようになります。
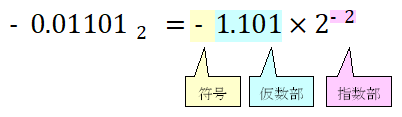
+0.01101から小数点を右に2桁動かすと+1.101になるので指数部の値は-2となります。
固定小数点型(数値型)
通貨の単位や小数点以下の桁数を考慮した数値を表すことができる型。サイズは8バイトです。
ビット数を\(n\)としたとき、符号付き通貨型が扱える数値の範囲は以下の式で表すことができます。
\[ value_{min}=-2^{n-1} \\ value_{max}=2^{n-1}-1 \]通貨型
通貨型は64ビット(8バイト)の数値として整数形式で格納されます。
\[ value_{min}=-2^{64-1}=-9,223,372,036,854,775,808 \\ value_{max}=2^{64-1}-1=9,223,372,036,854,775,807 \]小数点の左側に15桁、右側に4桁の固定小数点を指定するために10,000でスケーリングされ、-922,337,203,685,477.5808~922,337,203,685,477.5807の範囲の値で使用されます。
小数第5位以下の値を指定した場合は四捨五入されます。
Empty/Empty
Emptyはエンプティと読み、変数が初期化されていない状態を示します。変数や空の配列を宣言だけ行ったときは初期値として組み込み定数のEMPTYが代入されます。
以下はVARTYPE関数 (スクリプト関数)で引数に指定した値の型を調べるプログラムです。結果はすべてEMPTYを表す0を返します。
DIM str
PRINT VARTYPE(str) // Empty
DIM array[0]
PRINT VARTYPE(array[0]) // Empty
PRINT VARTYPE(EMPTY) // EmptyLENGTHで文字列の長さを取得すると0を返します。
PRINT LENGTH(EMPTY) // 0INPUT関数 (スクリプト関数)でキャンセル、☒を選択したときにもEMPTYを返します。
Null/Null
Nullはヌルもしくはナルと読み、Emptyは値が代入されていない未設定状態を表していたのに対して、Nullは値が無い状態を表します。
Emptyは変数の宣言時に初期値として代入されますが、Nullは意図的に代入しないと設定されることはありません。
自作関数で返す値がないときに設定するくらいであまり使われることはないです。
以下はstrにNULLを設定するプログラムです。
DIM str = NULLLENGTHで文字列の長さを取得すると1を返します。
PRINT LENGTH(NULL) // 12バイト整数(符号付き)/SmallInt
2バイト整数(符号付き)とは、符号付き整数型の一種で2バイト(16ビット)のデータ型で表現できる整数のことです。先頭ビットが値の正負を表す符号ビットで、残りの15ビットが数を表します。
- 範囲
- \({-32,768}_{(10)} 〜 {32,767}_{(10)}\)
- 最大値
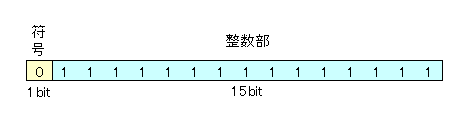 \[0111~1111~1111~1111_{(2)}={2^{15}-1}_{(10)}=32767_{(10)}\]
\[0111~1111~1111~1111_{(2)}={2^{15}-1}_{(10)}=32767_{(10)}\]- 最小値
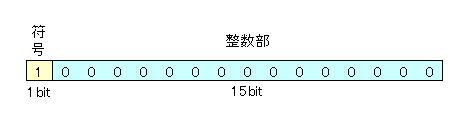 \[1000~0000~0000~0000_{(2)}={-2^{15}}_{(10)}=-32768_{(10)}\]
\[1000~0000~0000~0000_{(2)}={-2^{15}}_{(10)}=-32768_{(10)}\]
4バイト整数(符号付き)/Integer
4バイト整数(符号付き)とは、符号付き整数型の一種で4バイト(32ビット)のデータ型で表現できる整数のことです。先頭ビットが値の正負を表す符号ビットで、残りの31ビットが数を表します。
- 範囲
- \({-2,147,483,648}_{(10)} ~ {2,147,483,647}_{(10)}\)
- 最大値
-
 \[0111~1111~1111~1111~1111~1111~1111~1111 _{(2)}={2^{32}-1}_{(10)}={2147483647}_{(10)}\]
\[0111~1111~1111~1111~1111~1111~1111~1111 _{(2)}={2^{32}-1}_{(10)}={2147483647}_{(10)}\]
- 最小値
-
 \[1000~0000~0000~0000~0000~0000~0000~0000 _{(2)}={-2^{32}}_{(10)}={-2147483648}_{(10)}\]
\[1000~0000~0000~0000~0000~0000~0000~0000 _{(2)}={-2^{32}}_{(10)}={-2147483648}_{(10)}\]
単精度浮動小数点数/Single
- 正の値
- \({1.1754944 \times 10^{-38}}_{(10)}\) ~ \({3.40282339717 \times 10^{38}}_{(10)}\)
- 負の値
- \({-3.40282339717 \times 10^{38}}_{(10)}\) ~ \({-1.1754944 \times 10^{-38}}_{(10)}\)
 \[(-1)^{\mathrm{sign}} \times 2^{\mathrm{exponent} - \mathrm{exponent}\ \ \mathrm{bias}} \times 1.\mathrm{mantissa}\]
\[(-1)^{\mathrm{sign}} \times 2^{\mathrm{exponent} - \mathrm{exponent}\ \ \mathrm{bias}} \times 1.\mathrm{mantissa}\]
- \(\mathrm{sign}:符号\)
- \(\mathrm{exponent}:指数部\)
- \(\mathrm{exponent} \mathrm{bias}:指数部バイアス\)
- \(\mathrm{mantissa}:仮数部\)
- \(s:符号部\)
- \(xxx:仮数部\)
- \(yyy:指数部\)
- 符号ビット
- 1ビット
- 指数部の幅
- 8ビット(ゲタ履き表現)
- 仮数部の幅
- 23ビット
- 有効桁数
- \(\log_{10} 2^{23} = 23\log_{10} 2 = 23 * 0.301029957 = 6.923\)
符号ビットは表現する数値の符号(正負)を示します。指数部は8ビットで、符号なし整数として見た場合は0~255の値をとり、0のときは0か非正規化数であることを、1~254のときは-127のゲタ履き(バイアス付き)表現で-126~127の指数を、255のときは無限大またはNaNであることを示します。
指数部が0(0および非正規化数)の場合を除き、仮数部で表現されるビットパターンのさらにひとつ上の桁に暗黙の1のビットがあるとみなす表現法(ケチ表現)により、正規化された数の精度は、24ビットである。十進に換算したときに表現できる桁数は\(\log_{10} 2^{24} \approx 7.225\)桁となります。
指数部の符号化方式
単精度浮動小数点数の指数部はオフセット(ゲタ履き)表現を使って符号化されており、指数値が0のときオフセット値(バイアス値)は127である。
- \(E_{min}=01_{H}-7F_{H}=-126\)
- \(E_{max}=FE_{H}-7F_{H}=127\)
- \(exponent\ \ bias(指数バイアス)={7F}_{H}=127\)
\(00_{H}\)と\(FF_{H}\)は予約された指数値です。
正の最小値(単精度)

- 符号
- \((-1)^{0}\)
- 仮数部
- \(xxx = 000~0000~0000~0000~0000~0000\)
\(1.xxx=1.00000000000000000000000_{(2)}={2^{0}}_{(10)}=1.0_{(10)}\) - 指数部
- \(yyy = 0000~0001_{(2)}=1_{(10)}\)
\({2^{1-127}}_{(10)}={2^{-126}}_{(10)}\)=\({\frac{1}{2^{126}}}_{(10)}\)=\({1.1754944\times10^{-38}}_{(10)}\) - 符号×仮数部×指数部
- \[ \begin{eqnarray} value_{min}&=&(-1)^{0} \times 1 \times \frac{1}{2^{126}}\\ &=&1.175494351 \times 10^{-38} \end{eqnarray} \]
正の最大値(単精度)

- 符号
- \((-1)^{0}\)
- 仮数部
- \(xxx = 111~1111~1111~1111~1111~1111_{(2)}\)
\(1.xxx=1.11111111111111111111111\)
\[2^{0},2^{-1},2^{-2},…,2^{-23}\]- \(初項:a=1\)
- \(公比:r=0.5\)
- \(項数:n=24\)
- 指数部
- \(yyy = 1111~1110_{(2)}=254\)
\({2^{254-127}}_{(10)} = {2^{127}}_{(10)}={1.7014118\times10^{38}}_{(10)}\) - 符号×仮数部×指数部
- \[ \begin{eqnarray} value_{max}&=&(-1)^{0} \times \frac{1-0.5^{24}}{0.5} \times 2^{127} \\ &=&3.4028235 \times 10^{38} \end{eqnarray} \]
負の最小値(単精度)

- 符号
- \((-1)^{1}\)
- 仮数部
- \(xxx = 111~1111~1111~1111~1111~1111_{(2)}\)
\(1.xxx=1.11111111111111111111111_{(2)}\)
\(S=\frac{a(a-r^{n})}{1-r}=\frac{1-0.5^{24}}{1-0.5}=\frac{1-0.5^{24}}{0.5}=1.99999988079_{(10)}\) - 指数部
- \(yyy = 1111~1110_{(2)}=254\)
\({2^{254-127}}_{(10)}={2^{127}}_{(10)}=1.7014118 \times {10^{38}}_{(10)}\) - 符号×仮数部×指数部
- \[ \begin{eqnarray} value_{min}&=&(-1)^{1} \times \frac{1-0.5^{24}}{0.5} \times 2^{127}\\ &=&-3.4028235 \times 10^{38} \end{eqnarray} \]
負の最大値(単精度)

- 符号
- \((-1)^{1}\)
- 仮数部
- \(xxx = 000~0000~0000~0000~0000~0000_{(2)}\)
\(1.xxx=1.00000000000000000000000_{(2)}\)
\({2^{0}}_{(10)}=1.0_{(10)}\) - 指数部
- \(yyy = 0000~0001_{(2)}\)
\({2^{1-127}}_{(10)}={2^{-126}}_{(10)}\)=\({\frac{1}{2^{126}}}_{(10)}\)=\({1.1754944\times10^{-38}}_{(10)}\) - 符号×仮数部×指数部
- \[ \begin{eqnarray} value_{max}&=&(-1)^{1} \times 1.0 \times \frac{1}{2^{126}} \\ &=&-1.175494351 \times 10^{-38} \end{eqnarray} \]
倍精度浮動小数点数/Double
- 範囲(正の値)
- \(4.94065645841247 \times 10^{-324} ~ 1.79769313486232 \times 10^{308}\)
- 範囲(負の値)
- \(-1.79769313486232 \times 10^{308} ~ -4.94065645841247 \times 10^{-324}\)
- \(\mathrm{sign}:符号\)
- \(\mathrm{exponent}:指数部\)
- \(\mathrm{exponent} \mathrm{bias}:指数部バイアス\)
- \(\mathrm{mantissa}:仮数部\)
- 符号
- 1ビット
- 指数部(ゲタ履き表現)
- 11ビット(-1022~1023)
- 仮数部
- 52ビット
- 有効桁数
- \(\log_{10} 2^{52} = 52\log_{10} 2 = 52 * 0.301029957 = 15.653\)
指数部の符号化方式
倍精度浮動小数点数の指数部はオフセット(ゲタ履き)表現を使って符号化されており、指数値が0のときオフセット値(バイアス値)は1023である。
- \(E_{min}=01_{H}-3FF_{H}=-1022\)
- \(E_{max}=7FE_{H}-3FF_{H}=1024\)
- \(exponent\ \ bias(指数バイアス)={3FF}_{H}=1023\)
\(00_{H}\)と\(FF_{H}\)は予約された指数値です。
正の最小値(倍精度)

- 符号
- \((-1)^{0}=+1\)
- 仮数部
- \(xxx=0000~0000~0000~0000~0000~0000~0000~0000~0000~0000~0000~0000~0000\)
\(1.xxx=1.0000000000000000000000000000000000000000000000000000\)
\(2^{0}\times1+2^{-1}\times0+2^{-2}\times0+2^{-3}\times0+…+2^{-52}\times0=2.0\) - 指数部
- \({2^{1-1023}}_{(10)}={2^{-1022}}_{(10)}=2.225074 \times 10^{-308}\)
- 符号×仮数部×指数部
- \[ \begin{eqnarray} value_{min}&=&(-1)^{0} \times 2.0 \times 2^{-1022} \\ &=&4.450148 \times 10^{-308} \\ \end{eqnarray} \]
正の最大値(倍精度)

- 符号
- \((-1)^{0}=+1\)
- 仮数部
- \(xxx=1111~1111~1111~1111~1111~1111~1111~1111~1111~1111~1111~1111~1111\)
\(1.xxx=1.1111111111111111111111111111111111111111111111111111\)
\[2^{0} \times 1, \quad 2^{-1} \times 1, \quad 2^{-2} \times 1, \quad 2^{-3} \times 1, \quad …, \quad 2^{-52} \times 1\] \[S=\frac{a(1-r^n)}{1-r}=\frac{1 \times (1-0.5^{53})}{1-0.5}=2.0\] - 指数部
- \({2^{2046-1023}}_{(10)}={2^{1023}}_{(10)}=8.988466\times10^{307}\)
- 符号×仮数部×指数部
- \[ \begin{eqnarray} value_{max}&=&(-1)^{0} \times 2.0 \times 2^{1023}\\ &=&1.7976932 \times 10^{308} \\ \end{eqnarray} \]
負の最小値(倍精度)

- 符号
- \((-1)^{1}=-1\)
- 仮数部
- \(xxx=1111~1111~1111~1111~1111~1111~1111~1111~1111~1111~1111~1111~1111\)
\(1.xxx=1.1111111111111111111111111111111111111111111111111111\)
\[2^{0} \times 1, \quad 2^{-1} \times 1, \quad 2^{-2} \times 1, \quad 2^{-3} \times 1, \quad …, \quad 2^{-52} \times 1\] \[S=\frac{a(1-r^n)}{1-r}=\frac{1 \times (1-0.5^{53})}{1-0.5}=2.0\] - 指数部
- \({2^{2046-1023}}_{(10)}={2^{1023}}_{(10)}=8.988466\times10^{307}\)
- 符号×仮数部×指数部
- \[ \begin{eqnarray} value_{min}&=&(-1)^{1} \times 2.0 \times 2^{1023} \\ &=&-1.7976932 \times 10^{308} \\ \end{eqnarray} \]
負の最大値(倍精度)

- 符号
- \((-1)^{1}=-1\)
- 仮数部
- \(xxx=0000~0000~0000~0000~0000~0000~0000~0000~0000~0000~0000~0000~0000\)
\(1.xxx=1.0000000000000000000000000000000000000000000000000000\)
\(2^{0} \times 1+2^{-1} \times 0+2^{-2} \times 0+2^{-3} \times 0+…+2^{-52} \times 0=2.0\) - 指数部
- \({2^{1-1023}}_{(10)}={2^{-1022}}_{(10)}=2.225074 \times 10^{-308}\)
- 符号×仮数部×指数部
- \[ \begin{eqnarray} value_{max}&=&(-1)^{1} \times 2.0 \times 2^{-1022} \\ &=&-4.450148 \times 10^{-308} \\ \end{eqnarray} \]
通貨型/Currency
64ビット(8バイト)の数値として整数形式で格納され、小数点の左側に15桁、右側に4桁の固定小数点番号を指定するために10,000でスケーリングされます。
正の最小値

正の最大値

- 符号
- \((-1)^{0}=1\)
- 整数部
- \(2^{63}-1=9,223,372,036,854,775,807\)
実際使うときは1/10000倍する。
\(922,337,203,685,477.5807\)
負の最小値

- 符号
- \((-1)^{1}=1\)
- 整数部
- \(-2^{63}=-9,223,372,036,854,775,808\)
実際使うときは1/10000倍する。
\(-922,337,203,685,477.5808\)
負の最大値

通貨型変数(Currency)は整数部15桁、小数部4桁の固定小数点型変数です。内部的には10000倍されて19桁の整数として記憶されます。
-922,337,203,685,477.5808 ~ 922,337,203,685,477.5807日付型/Date
日付・時刻・日時を扱うための型です。整数部分が日付、小数部分が時刻を表しています。
- 範囲
- -657,434 ~ 2,958,465(100/01/01 ~ 9999/12/31)
PRINT VARTYPE(-657434, VAR_DATE) // 100/01/01
PRINT VARTYPE(2958465, VAR_DATE) // 9999/12/310以上1未満の値を指定した場合は時刻のみ出力されます。
PRINT VARTYPE(0, VAR_DATE) // 00:00:00
PRINT VARTYPE(0.0416666666666666, VAR_DATE) // 01:00:00
PRINT VARTYPE(0.5, VAR_DATE) // 12:00:00
PRINT VARTYPE(0.999988425925926, VAR_DATE) // 23:59:590は時刻を返すので1899/12/30という日付を返すことは出来ません。
PRINT VARTYPE(-1, VAR_DATE) // 1899/12/29
PRINT VARTYPE(0, VAR_DATE) // 00:00:00
PRINT VARTYPE(1, VAR_DATE) // 1899/12/31小数の値を指定すると日時を返します。
PRINT VARTYPE(45776.5, VAR_DATE) // 2025/04/29 12:00:00
PRINT VARTYPE(45780.125, VAR_DATE) // 2025/05/03 03:00:00オブジェクト型/Dispatch
オブジェクト型とは、データを扱うための型の一種でデータとそれに関連する処理(メソッド)を一つの単位としてまとめたものです。UWSCではCREATEOLEOBJ関数 (スクリプト関数)で作成することができ変数にはオブジェクトの値が入ります。
以下はShell オブジェクトを生成するプログラムです。
DIM Shell = CREATEOLEOBJ("Shell.Application")この値は生成されたCOMオブジェクトの参照を示すハンドル値(ポインタ)です。この値自体は特定の意味を持つわけではなく、プログラム内部でオブジェクトを管理するための識別子として使用されます。
オブジェクトの変数にNOTHINGを指定するとオブジェクトへの参照をなくすことで、メモリを解放することができます。
以下は生成したShell オブジェクトを解放するプログラムです。
Shell = NOTHINGブール型/Boolean
ブール型は真理値のTrue(真)またはFalse(偽)の2種類のみをとるデータ型です。制御文で条件式を書いたとき、このブール型の値(真または偽)に基づいて分岐されます。
ブール型を数値型に変換するとTrueは1、Falseは0となります。
PRINT VARTYPE(TRUE, VAR_BYTE) // 1
PRINT VARTYPE(FALSE, VAR_BYTE) // 0数値型をブール型に変換すると0がFalse、0以外の値はTrueとなります。
PRINT VARTYPE(1, VAR_BOOLEAN) // True
PRINT VARTYPE(0, VAR_BOOLEAN) // False
PRINT VARTYPE(-0, VAR_BOOLEAN) // False
PRINT VARTYPE(0.0, VAR_BOOLEAN) // False
PRINT VARTYPE(-0.0, VAR_BOOLEAN) // False
PRINT VARTYPE(2, VAR_BOOLEAN) // True
PRINT VARTYPE(1.5, VAR_BOOLEAN) // True
PRINT VARTYPE(5.7E+6, VAR_BOOLEAN) // True
PRINT VARTYPE(-1, VAR_BOOLEAN) // True
PRINT VARTYPE(-2.3, VAR_BOOLEAN) // True
PRINT VARTYPE(-9.6E-5, VAR_BOOLEAN) // True1バイト整数(符号付き)/SByte
1バイト整数(符号付き)とは、符号付き整数型の一種で1バイト(8ビット)のデータ型で表現できる整数のことです。先頭ビットが値の正負を表す符号ビットで、残りの7ビットが数を表します。
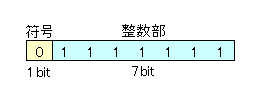
- 最大値
- \((-1)^{0} \times 2^{7}-1=127\)
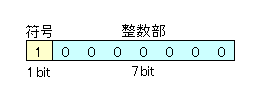
- 最小値
- \((-1)^{1} \times 2^{8}=-128\)
1バイト整数(符号なし)/Byte
1バイト整数(符号なし)とは、符号なし整数型の一種で1バイト(8ビット)のデータ型で表現できる整数のことです。8ビット全てを数値の表現に使います。
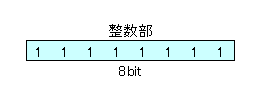
- 最大値
- \(2^{8}-1=255\)
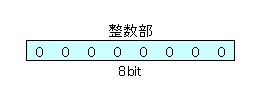
- 最小値
- 0
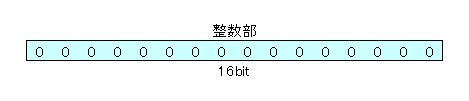
2バイト整数(符号なし)/Word
2バイト整数(符号なし)とは、符号なし整数型の一種で2バイト(16ビット)のデータ型で表現できる整数のことです。16ビット全てを数値の表現に使います。
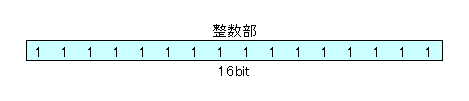
- 最大値
- \(2^{16}-1=65535\)
- 最小値
- 0
4バイト整数(符号なし)/DWord
4バイト整数(符号なし)とは、符号なし整数型の一種で4バイト(32ビット)のデータ型で表現できる整数のことです。32ビット全てを数値の表現に使います。

- 最大値
- \(2^{32}=4,294,967,295\)

- 最小値
- 0
8バイト整数(符号付き)/Int64
8バイト整数(符号付き)とは、符号付き整数型の一種で8バイト(64ビット)のデータ型で表現できる整数のことです。先頭ビットが値の正負を表す符号ビットで、残りの63ビットが数を表します。

- 最大値
- \((-1)^{0} \times 2^{63}-1=9,223,372,036,854,775,807 \)

- 最小値
- \((-1)^{1} \times 2^{63}=-9,223,372,036,854,775,808\)
ANSI文字列/AStr
ANSIとはアメリカ国家規格協会(American National Standards Institute)の略称で、その言語・地域における標準規格を指しています。日本であればANSI文字列はShift_JIS(CP932)と同等です。ANSIで使える文字はShift_JISを参照してください。
Shift_JISに存在しない文字をShift_JISに変換すると文字化けを起こし?や??を返します。
PRINT VARTYPE("¼", VAR_ASTR) // ?
PRINT VARTYPE("🍏", VAR_ASTR) // ??
PRINT VARTYPE("안녕하세요", VAR_ASTR) // ?????UNICODE文字列/UStr
文字列を格納しておくための型です。UNICODE文字列の型に宣言した変数に10万文字格納してみても認識したため、格納する分だけ領域を確保するものと思われます。
配列/Array
| データ型 | 範囲 |
|---|---|
| Empty/Empty | |
| Null/Null | |
| 2バイト整数(符号付き)/SmallInt | -32,768~32,767 |
| 4バイト整数(符号付き)/Integer | -2,147,483,648 ~ 2,147,483,647 |
| 単精度浮動小数点値/Single |
-3.402823E+38 ~ -1.401298E-45(負の値) 1.401298E-45 ~ 3.402823E+38(正の値) |
| 倍精度浮動小数点値/Double |
-1.79769313486232E+308 ~ -4.94065645841247E-324(負の値) 4.94065645841247E-324 ~ 1.79769313486232E+308(正の値) |
| 通貨型/Currency | -922,337,203,685,477.5808 ~ 922,337,203,685,477.5807 |
| 日付型/Date | -657,434 ~ 2,958,465(100/01/01 ~ 9999/12/31) |
| オブジェクト/Dispatch | |
| エラー値/Error | |
| ブール型/Boolean | |
| バリアント/Variant | |
| 未定義のオブジェクト/Unknown | |
| 1バイト整数(符号付き)/SByte | -128 ~ 127 |
| 1バイト整数(符号なし)/Byte | 0 ~ 255 |
| 2バイト整数(符号なし)/Word | 0 ~ 65,535 |
| 4バイト整数(符号なし)/DWord | 0 ~ 4,294,967,295 |
| 8バイト整数(符号付き)/Int64 | -9,223,372,036,854,775,808 ~ 9,223,372,036,854,775,807 |
| ANSI文字列/AStr | |
| UNICODE文字列/UStr | |
| 配列/Array |
使い方
INFはINFinityの略で無限大を表し、オーバーフローが発生したときに表示されます。
DIM n // Double型
n = POWER(2, 1024) // 2^1024
PRINT n
IF n = "INF" THEN PRINT TRUE- 結果
INF True
負の値でも同様です。
DIM n // Double型
n = -1 * POWER(2, 1024) // -2^1024
PRINT n
IF n = "-INF" THEN PRINT TRUE- 結果
-INF True
倍精度浮動小数点数で格納できる最大値。
DIM n
n = POWER(2, 1023) * 1.9999999999
PRINT n- 結果
1.79769313477243E308
型変換時にオーバーフローする例。
DIM n // 倍精度浮動小数点数で宣言
n = 32768
n = VARTYPE(n, VAR_SMALLINT) // 2バイト整数(符号付き)に型変換"Double型をSmallInt型に変換する際にオーバーフローしました"というようなメッセージが出ます。「2バイト整数」では格納できる最大値が32,767なのでそれ以上の値が入っている状態で型変換するとオーバーフローします。
KansuCall:Overflow while converting variant of type (Double) into type (SmallInt)型変換
変数の型を変換するにはVARTYPE関数 (スクリプト関数)を使います。
型変換前の値が変換後で扱える範囲を超える場合、型変換によるオーバーフローのエラーが発生します。
以下は2バイト整数(符号なし)から1バイト整数(符号なし)へ変換する例。変換先が1バイト整数で扱える範囲を超えているのでエラーが発生します。
DIM x = VARTYPE(10000, VAR_WORD) // 符号なし2バイト整数(0~65,535)
PRINT VARTYPE(x, VAR_BYTE) // 符号なし1バイト整数(0~255)以下の表は、左の項目を上の項目に変数で型変換できるかを示したものです。変換できる場合は✓、できない場合は✕です。
| Empty | Null | SmallInt | Integer | Single | Double | Currency | Date | Dispatch | Error | Boolean | Variant | Unknown | Sbyte | Byte | Word | Dword | Int64 | Astr | Ustr | Array | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Empty | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Null | ✕ | ✓ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ |
| SmallInt | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Integer | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Single | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Double | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Currency | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Date | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Dispatch | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✓ | ✓ | ✕ |
| Error | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Boolean | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Variant | |||||||||||||||||||||
| Unknown | |||||||||||||||||||||
| Sbyte | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Byte | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Word | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Dword | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Int64 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Astr | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Ustr | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✕ |
| Array | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ |
文字列→数値
+という演算子は加算演算子として使われますが、文字列の場合は連結演算子として使われます。以下は100 + 23の計算をするプログラムですが、100が文字列なので、結合演算子として使われ100と23が結合されます。
DIM str = "100"
PRINT str + 23- 結果
10023
strが文字列なのでVARTYPE関数 (スクリプト関数)で数値に変換する必要があります。整数の場合はVAR_INTEGER、小数の場合はVAR_DOUBLEを第二引数に指定します。整数でVAR_DOUBLEを指定する分には問題ありませんが、小数でVAR_INTEGERを使うと小数点以下が丸められるので注意が必要です。
DIM str = "100"
PRINT VARTYPE(str, VAR_INTEGER) + 23- 結果
123
VARTYPE関数 (スクリプト関数)は変換先の型を指定しなければなりませんが、VAL関数 (スクリプト関数)を使うと変換元が整数か小数に関係なく、また型を指定しなくても計算に使える数値に変換してくれます。
DIM str = "100"
DIM num = VAL(str) + 23- 結果
123
数値→文字列
数値から文字列に変換するには、VARTYPE関数 (スクリプト関数)を使用する他に連結演算子を使う方法があります。
numには数値の型として123を代入していますが、strには、空文字列である""と結合し文字列型に変換した値を代入しています。
連結演算子は左項もしくは右項のどちらかが文字列の場合、文字列型として結合されることを利用しています。
DIM num = 123
DIM str = "" + num数値→日付
1899/12/30からの経過日数を出力します。整数部分が日付、小数部分が時刻を表しています。
PRINT VARTYPE(45292, VAR_DATE)
PRINT VARTYPE(1, VAR_DATE)
PRINT VARTYPE(-1, VAR_DATE)
PRINT VARTYPE(45000.4, VAR_DATE)- 結果
2024/01/01 1899/12/31 1899/12/29 2023/03/15 09:36:00
0以上1未満の数値を指定した場合は、時刻のみ出力します。
PRINT VARTYPE(0, VAR_DATE)
PRINT VARTYPE(0.8, VAR_DATE)- 結果
00:00:00 19:12:00
オブジェクト型→文字列型
DIM IE = CREATEOLEOBJ("InternetExplorer.Application")
PRINT VARTYPE(IE, VAR_USTR)
IE.Quit- 結果
Internet Explorer
DIM Excel = CREATEOLEOBJ("Excel.Application")
PRINT VARTYPE(Excel, VAR_USTR)
Excel.Quit- 結果
Microsoft Excel
DIM Word = CREATEOLEOBJ("Word.Application")
PRINT VARTYPE(Word, VAR_USTR)
Word.Quit- 結果
Microsoft Word
DIM Outlook = CREATEOLEOBJ("Outlook.Application")
PRINT VARTYPE(Outlook, VAR_USTR)
Outlook.Quit- 結果
Outlook
参考文献
- 【VBA】Currency(通貨型変数)
- Ispirer Toolkitのユーザーガイド(日本語版) - Ispirer Knowledge Base
- 負数/補数-2進数と遊ぶ(1000)
- http://ss.sguc.ac.jp/~rider/basic/interger.html
- https://ja.wikipedia.org/wiki/%E5%A4%89%E6%95%B0_
- "ANSI"とは何か?【文字コード周りの話】 : LIFE IS MIRACLE WIND
