引数の逆余弦を求めます。
- 構文
- Double = ARCCOS( 数値 )
- 引数
- 数値 （Single）必須
- -1〜1の範囲の数値。範囲外の数値を指定するとNANが返ります。
- 戻り値
- 数値の逆余弦（ラジアン単位）
戻り値は\(0\)〜\(\pi\)（0°〜180°）の範囲の値です。
逆余弦関数
\( y = \cos x \)の逆関数のことを逆余弦関数（アークコサイン）といい、\( y = \arccos x \)または\( y = \cos^{-1} x \)で表します。
余弦関数（\( \cos x \)）は角度\( x \)という直角三角形において、斜辺と隣辺の2辺の比を求めるのに対し、逆余弦関数（\( \arccos x \)）はこの2辺の比から角度を求めます。
以下は\( y = \cos x \)のグラフ。横軸が\( x \)、縦軸が\( y \)を表しています。
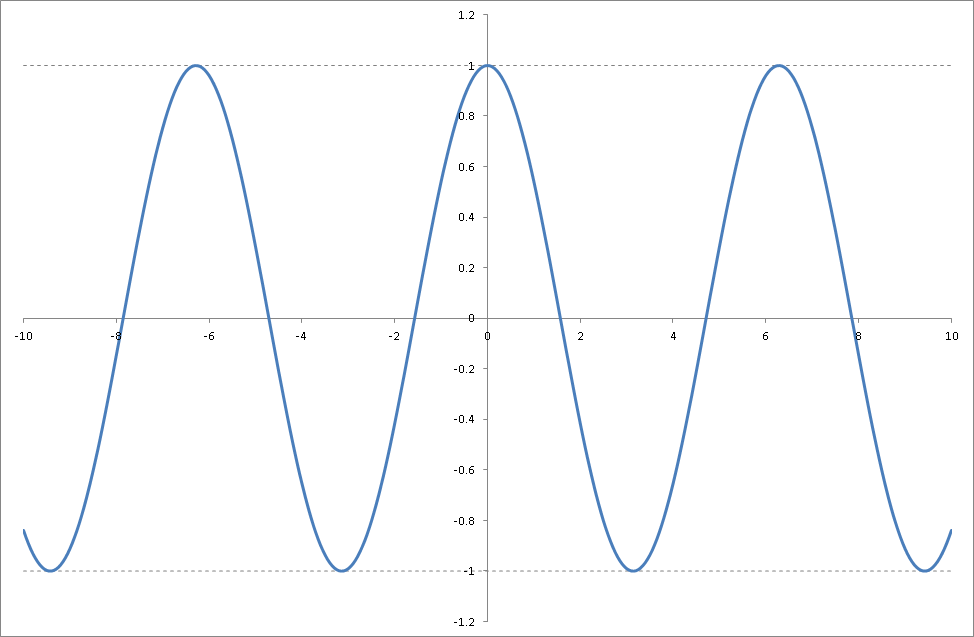
cos関数は\( -1 \leq x \leq 1 \)の間の値を何度も取るため\( x \)が決まれば\( y \)の値は一つに決まるが、\( y \)の値から求まる\( x \)の値は一つにはなりません。
例えば\( \cos \frac{\pi}{3} = \frac{1}{2} \)、\( \cos \frac{5}{3} \pi = \frac{1}{2} \)のように、\( y = \frac{1}{2} \)となる\( x \)の値は複数あります。
一般に\( x \)の範囲を限定せずに\( y = \cos x \)の逆関数\( x = \arccos y \)を定義すると、1つの\( y \)の値に対して無限個の\( x \)の値が対応する多価関数となります。
そこで\( y=\arccos x \)の逆関数がただ1つに定まるように、\( 0 \leq y \leq \pi \)の範囲で考え、この値のことを主値といいます。
\[ y = \cos x \qquad (0 \leq x \leq \pi, -1 \leq y \leq 1 ) \\ \leftrightarrow x = \arccos y \qquad ( -1 \leq y \leq 1, 0 \leq x \leq \pi ) \]独立変数を\( x \)、従属変数を\( y \)で置き換えると以下のようになります。
\[ y = \arccos x \qquad ( -1 \leq x \leq 1, 0 \leq y \leq \pi ) \]\(y=\arccos x\)の定義域は\(-1 \leq x \leq 1\)、値域は\( 0 \leq y \leq \pi \)となります。
引数と戻り値の範囲はこの定義域と値域を表しています。
以下は\( x = \cos y \)（\( y = \arccos x \)）のグラフを表しています。
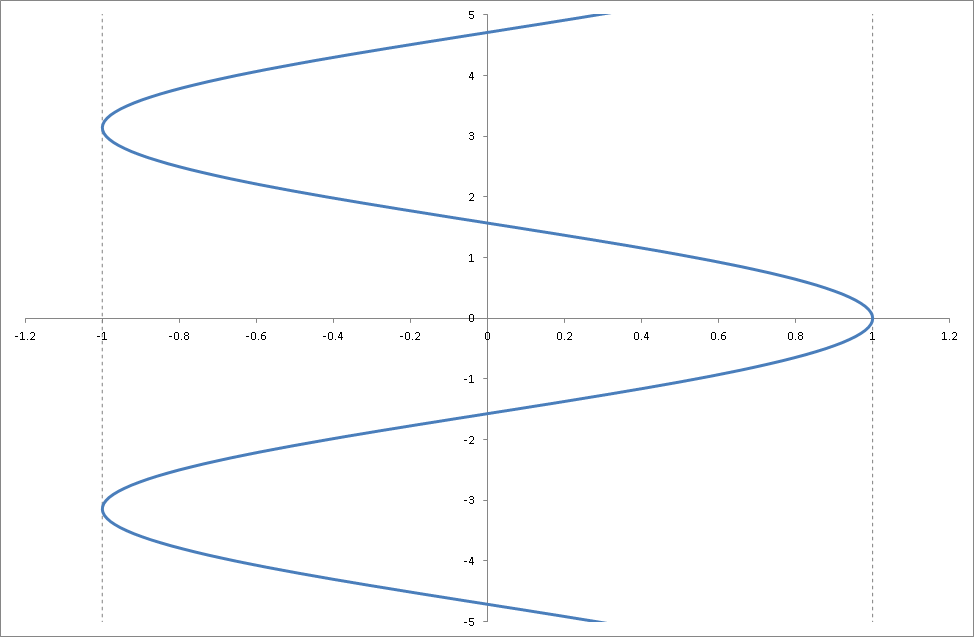
以下は\( y = \arccos x \)のグラフから主値の範囲（\( 0 \leq y \leq \pi \)）だけ抽出したグラフ。これがARCCOS関数で求められる数値をグラフで表したものです。
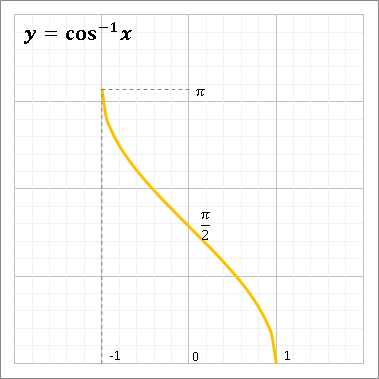
使い方
PRINT ARCCOS(-1)
PRINT radToDeg(ARCCOS(-1))
PRINT ARCCOS(0)
PRINT radToDeg(ARCCOS(0))
PRINT ARCCOS(1)
PRINT radToDeg(ARCCOS(1))
//////////////////////////////////////////////////
// 【引数】
// 数値 : 角度（弧度法）
// 【戻り値】
// 弧度法から度数法に変換します。
//////////////////////////////////////////////////
FUNCTION radToDeg(rad)
RESULT = rad * (180 / 3.14159265358979)
FEND- 結果
3.14159265358979 180 1.5707963267949 90.0000000000003 0 0
関連記事
- ARCSIN関数 (スクリプト関数)
- 引数の逆正弦を求めます。
- ARCTAN関数 (スクリプト関数)
- 引数の逆正接を求めます。
- radToDeg関数 (自作関数)
- 弧度法（Radian）を度数法（Degree）に変換します。度数法を弧度法に変換するにはDegToRad関数を使います。
- degToRad関数 (自作関数)
- 度数法（Degree）を弧度法（Radian）に変換します。弧度法を度数法に変換するにはRadToDeg関数を使います。
- COS関数 (スクリプト関数)
- 引数の余弦を求めます。
- SIN関数 (スクリプト関数)
- 引数の正弦を求めます。
- TAN関数 (スクリプト関数)
- 引数の正接を求めます。
- ABS関数 (スクリプト関数)
- 引数の絶対値を求めます。
- CEIL関数 (スクリプト関数)
- 正の方向へ切り上げた数値を返します。
- LN関数 (スクリプト関数)
- 自然対数を求めます。