引数の逆正弦を求めます。
- 構文
- Double = ARCSIN( 数値 )
- 引数
- 数値 （Single）必須
- -1〜1の範囲の数値。範囲外の数値を指定するとNANが返ります。
- 戻り値
- 数値の逆正弦（ラジアン単位）
戻り値は\(-\frac{\pi}{2}\)〜\(\frac{\pi}{2}\)（-90°〜90°）の範囲の値です。
逆正弦関数
\(y=\sin x\)の逆関数のことを逆正弦関数（アークサイン）といい、\(y=\arcsin x\)または\(y=\sin^{-1} x\)で表します。
正弦関数（\( \sin x \)）は角度\( x \)という直角三角形において、斜辺と対辺の2辺の比を求めるのに対し、逆正弦関数（\( \arcsin x \)）はこの2辺の比から角度を求めます。
以下は\( y = \sin x \)のグラフ。横軸が\( x \)、縦軸が\( y \)を表しています。
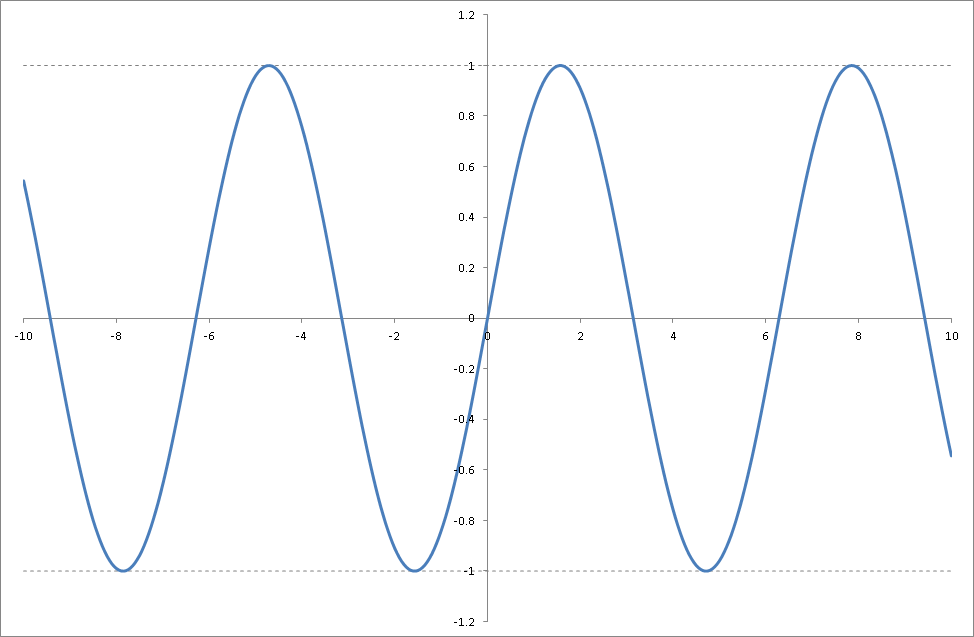
sin関数は\(-1 \leq x \leq 1\)の間の値を何度も取るため\(x\)が決まれば\( y \)の値は一つに決まるが、\(y\)の値から求まる\( x \)の値は一つにはなりません。
例えば\( \sin \frac{\pi}{6} = \frac{1}{2} \)、\( \sin \frac{5}{6} \pi = \frac{1}{2} \)のように、\( y = \frac{1}{2} \)となる\( x \)の値は複数あります。
一般に\( x \)の範囲を限定せずに\( y = \sin x \)の逆関数\( x = \arcsin y \)を定義すると、1つの\( y \)の値に対して無限個の\( x \)の値が対応する多価関数となります。
そこで\(y=\arcsin x\)の逆関数がただ1つに定まるように、\(-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}\)の範囲で考え、この値のことを主値といいます。
\[ y = \sin x \qquad (-\frac{\pi}{2} \leq x \leq \frac{\pi}{2}, -1 \leq y \leq 1 ) \\ \leftrightarrow x = \arcsin y \qquad ( -1 \leq y \leq 1, -\frac{\pi}{2} \leq x \leq \frac{\pi}{2} ) \]独立変数を\( x \)、従属変数を\( y \)で置き換えると以下のようになります。
\[ y = \arcsin x \qquad ( -1 \leq x \leq 1, -\frac{\pi}{2} \leq y \leq \frac{\pi}{2} ) \]\( y=\arcsin x \)の定義域は\( -1 \leq x \leq 1 \)、値域は\( -\frac{\pi}{2} \leq y \leq \frac{\pi}{2} \)となります。
引数と戻り値の範囲はこの定義域と値域を表しています。
以下は\( x = \sin y \)（\( y = \arcsin x \)）のグラフを表しています。
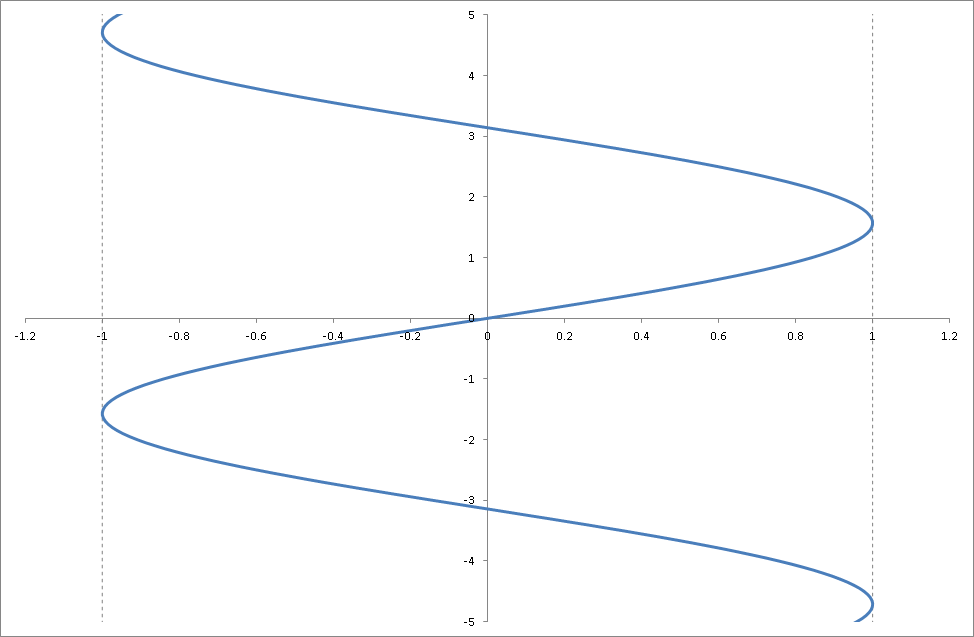
以下は\( y = \arcsin x \)のグラフから主値の範囲（\( -\frac{\pi}{2} \leq y \leq \frac{\pi}{2} \)）だけ抽出したグラフ。これがARCSIN関数で求められる数値をグラフで表したものです。
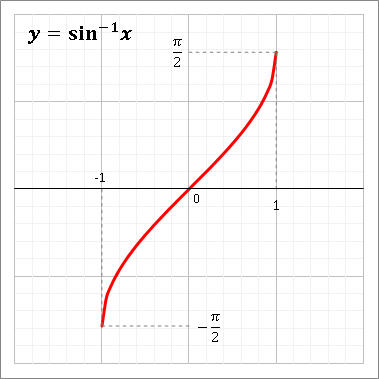
ARCSIN関数の引数がグラフの横軸、戻り値が縦軸となります。ARCSIN(1)の結果が-1.5707963267949（\( -\frac{\pi}{2} \)）とグラフの値と一致しているのがわかると思います。
- Main
- FUNCTIONS
PRINT ARCSIN(-1)
PRINT radToDeg(ARCSIN(-1))//////////////////////////////////////////////////
// 【引数】
// 数値 : 角度（弧度法）
// 【戻り値】
// 弧度法から度数法に変換します。
//////////////////////////////////////////////////
FUNCTION radToDeg(rad)
RESULT = rad * (180 / 3.14159265358979)
FEND- 結果
-1.5707963267949 -90.0000000000003
以下は\( x = 0 \)のとき。
PRINT ARCSIN(0)
PRINT radToDeg(ARCSIN(0))- 結果
0 0
以下は\( x = 1 \)のとき。
PRINT ARCSIN(1)
PRINT radToDeg(ARCSIN(1))- 結果
1.5707963267949 90.0000000000003
逆関数の性質により、SIN関数で求められた結果をARCSIN関数の引数に指定すると元に戻ります。
PRINT ARCSIN(SIN(0.5))- 結果
0.5
参考文献
関連記事
- ARCCOS関数 (スクリプト関数)
- 引数の逆余弦を求めます。
- ARCTAN関数 (スクリプト関数)
- 引数の逆正接を求めます。
- radToDeg関数 (自作関数)
- 弧度法から度数法に変換します。
- degToRad関数 (自作関数)
- 度数法から弧度法に変換します。
- SIN関数 (スクリプト関数)
- 引数の正弦を求めます。
- COS関数 (スクリプト関数)
- 引数の余弦を求めます。
- TAN関数 (スクリプト関数)
- 引数の正接を求めます。
- ABS関数 (スクリプト関数)
- 引数の絶対値を求めます。
- CEIL関数 (スクリプト関数)
- 正の方向へ切り上げた数値を返します。
- LN関数 (スクリプト関数)
- 自然対数を求めます。